Ленивые вычисления¶
В ленивых вычислениях каждый элемент данных вычисляется тогда, когда он понадобился, а не заранее. Эта техника позволяет работать с потенциально бесконечными структурами данных. В каждый момент времени имеется только конечное число их элементов, которые уже были зачем-то нужны. Если потом понадобятся ещё какие-нибудь элементы этой структуры данных, то они тоже будут вычислены и запомнены.
Например, ряд Тэйлора - это бесконечный список коэффициентов. В некоторых системах компьютерной алгебры (Axiom и его форки, Reduce) реализованы ленивые ряды. Ленивый ряд - это список нескольких первых коэффициентов плюс алгоритм, позволяющий вычислять дальнейшие коффициенты, если они понадобятся. Допустим, пользователь произвёл какое-то вычисление с рядами и получил несколько первых членов ряда-результата. Если он захочет увидеть несколько следующих членов, он может просто запросить их у этого ленивого ряда-результата - нет необходимости повторять всё вычисление. В большинстве систем компьютерной алгебры (Mathematica, Maple и т.д.) ряд Тэйлора - это конечный список коэффициентов плюс остаточный член $O(x^n)$, показывающий, с какой точностью этот ряд известен. Если пользователь получил ряд-результат, но не доволен его точностью, ему придётся разложить все исходные функции до большего числа членов и затем повторить вычисление. Причём в сложных случаях трудно догадаться, какие исходные функции нужно разложить докуда для получения результата с желаемой точностью.
Мы сейчас напишем программу на питоне для работы с ленивыми рядами Тэйлора с рациональными коэффициентами. Класс Series - корень иерархии классов для таких рядов. Каждый объект s этого класса (или его потомков) содержит список уже вычисленных коффициентов s.l; s[n] - это коффициент при $x^n$ (рациональное число, то есть объект класса Fraction). Можно пользоваться всеми прелестями питонской индексации, например, s[n:m], только не индексацией с конца (типа s[-1]), что естественно. Для этого реализован метод __getitem__; в случае s[n:m] он вызывается с аргументом slice(n,m). Если $n$-ый элемент ряда ещё не был вычислен, нужно несколько раз вызвать метод s.step(), который вычисляет следующие коффициенты и добавляет их в конец списка. Мы не хотим, чтобы пользователь мог произвольно менять коффициенты ряда, потому не реализуем __setitem__ (который вызывался бы в случаях s[n]=x или s[n,m]=[x,y,z]).
from fractions import Fraction
class Series:
"Базовый класс для ленивых рядов Тэйлора"
def __init__(self,l):
self.l=[Fraction(x) for x in l]
def __str__(self):
s=''
cont=False
for n,x in enumerate(self.l):
if x!=0:
s+=('+' if cont else '') if x>0 else '-'
xa=abs(x)
if xa!=1:
s+=str(abs(x))
s+='*x' if n>=1 else ''
else:
s+='x' if n>=1 else '1'
s+=f'^{n}' if n>1 else ''
cont=True
n=len(self.l)
s+=('+' if cont else '')+'O('+('x'+(f'^{n}' if n>1 else '') if n>0 else '1')+')'
return s
def __repr__(self):
return f'Series({self.l})'
def step(self):
self.l.append(0)
def __getitem__(self,n):
if isinstance(n,slice):
m=max(n.start,n.stop)
else:
m=n
while len(self.l)<=m:
self.step()
return self.l[n]
def __add__(self,x):
if isinstance(x,Series):
return Sum(self,x)
else:
return self+Series([x])
def __radd__(self,x):
if isinstance(x,Series):
return Sum(self,x)
else:
return self+Series([x])
def __sub__(self,x):
return self+(-x)
def __rsub__(self,x):
return (-self)+x
def __mul__(self,x):
if isinstance(x,Series):
return Product(self,x)
else:
return Product1(self,x)
def __rmul__(self,x):
if isinstance(x,Series):
return Product(self,x)
else:
return Product1(self,x)
def __neg__(self):
return Product1(self,-1)
def __call__(self,x):
return Apply(self,x)
def __pow__(self,n):
if n==0:
return Series([1])
elif n<0:
assert self[0]!=0
if isinstance(n,Fraction):
if n.denominator==1:
n=n.numerator
a,m=self.norm()
m*=n
if isinstance(m,Fraction):
assert m.denominator==1
m=m.numerator
return Shift(Pow(a,n),m)
def __truediv__(self,x):
if isinstance(x,Series):
a,n=self.norm()
b,m=x.norm()
assert n>=m
return Div(a,b).shift(n-m)
else:
return self*(Fraction(1)/x)
def __rtruediv__(self,x):
return x*self**(-1)
def inv(self):
return Inv(self)
def scale(self,c):
return Apply1(self,c)
def shift(self,n):
if n==0:
return self
else:
return Shift(self,n)
def norm(self,max=100):
m=0
while self[m]==0:
m+=1
assert m<=max
return (self.shift(-m),m)
def diff(self):
return Diff(self)
def int(self):
return Int(self)
Класс Series можно использовать сам по себе. Он означает полином, т.е. конечный ряд. Его методу __init__ передаётся список коффициентов. Метод step просто добавляет в конец списка нули.
s=Series([1,2])
print(s)
print(s[10])
print(s)
Классы для других рядов наследуют от Series и переопределяют метод step (а также ряд других методов). Вот ряд для экспоненты.
class Exp(Series):
"Ряд для exp(x)"
def __init__(self):
self.l=[Fraction(1)]
def __repr__(self):
return 'Exp()'
def step(self):
n=len(self.l)
self.l.append(self.l[-1]/n)
e=Exp()
print(e)
print(e[10])
print(e)
Ряды для косинуса и синуса устроены аналогично.
class Cos(Series):
"Ряд для cos(x)"
def __init__(self):
self.l=[Fraction(1)]
def __repr__(self):
return 'Cos()'
def step(self):
n=len(self.l)+1
self.l+=[0,-self.l[-1]/((n-1)*n)]
class Sin(Series):
"Ряд для sin(x)"
def __init__(self):
self.l=[0,Fraction(1)]
def __repr__(self):
return 'Sin()'
def step(self):
n=len(self.l)+1
self.l+=[0,-self.l[-1]/((n-1)*n)]
Вот ещё парочка простых рядов.
class Log(Series):
"Ряд для log(1+x)"
def __init__(self):
self.l=[0,Fraction(1)]
self.sign=1
def step(self):
n=len(self.l)
self.sign=-self.sign
self.l.append(Fraction(self.sign,n))
class Binom(Series):
"Ряд для (1+x)^n"
def __init__(self,n):
self.l=[Fraction(1)]
self.n=n
def __repr__(self):
return f'Binom({repr(self.n)})'
def step(self):
n=len(self.l)
self.l.append(self.l[-1]*Fraction((self.n-n+1),n))
Теперь реализуем сложение рядов. Центральный метод step вычисляет коффициент при $x^n$, который ещё не был известен. Для этого он складывает коффициеты при $x^n$ в рядах a и b. Если они ещё не были вычислены, то при вычислении a[n] будет вызван метод a.step(), а при вычислении b[n] - b.step().
class Sum(Series):
"Сумма рядов"
def __init__(self,a,b):
self.a=a
self.b=b
self.l=[a[0]+b[0]]
def __repr__(self):
return f'Sum({repr(self.a)},{repr(self.b)})'
def step(self):
n=len(self.l)
self.l.append(self.a[n]+self.b[n])
Произведение рядов реализовано аналогично, только формула для коэффициента при $x^n$ немного сложнее.
class Product(Series):
"Произведение рядов"
def __init__(self,a,b):
self.a=a
self.b=b
self.l=[a[0]*b[0]]
def __repr__(self):
return f'Product({repr(self.a)},{repr(self.b)})'
def step(self):
n=len(self.l)
self.l.append(sum(self.a[i]*self.b[n-i] for i in range(n+1)))
Если один из сомножителей не ряд, а число (рациональное или целое), ситуация упрощается.
class Product1(Series):
"Ряд умножить на число"
def __init__(self,a,b):
self.a = a
self.b = b
self.l=[a.l[i]*b for i in range(len(a.l))]
def __repr__(self):
return Product.__repr__(self)
def step(self):
n=len(self.l)
self.l.append(self.a[n]*self.b)
Возведение в степень (целую или рациональную) - более сложная операция. В некоторых случаях результат не является рядом Тэйлора. Например, если $a_0=0$, то при возведении ряда $a$ в отрицательную степень получится ряд Лорана, а у нас они не реализованы. При возведении в дробную степень может получиться ряд по дробным степеням $x$. Такие случаи отлавливаются операторами assert, и возбуждают исключения. В нормальном случае используется рекуррентное соотношение - коффициент $l_n$ при $x^n$ в ряде-результате выражается через уже вычисленные $l_m$ с $m<n$ (и, конечно, через $a_m$). Используются некоторые вспомогательные классы и функции, которые будут определены позже.
class Pow(Series):
"a^n"
def __init__(self,a,n):
self.a=a
self.n=n
a0=Fraction(a[0])
an,ad=a0.numerator,a0.denominator
if isinstance(n,Fraction):
nn,nd=n.numerator,n.denominator
an=pow1(an,nd)**nn
ad=pow1(ad,nd)**nn
a0=Fraction(an,ad)
else:
a0=a0**n
self.l=[a0]
def __repr__(self):
return f'Pow({repr(self.a)},{repr(self.n)})'
def step(self):
m=len(self.l)
self.l.append(sum((k*self.n-m+k)*self.a[k]*self.l[m-k] for k in range(1,m+1))/(m*self.a[0]))
Деление рядов реализовано похожим образом. Опять используется рекуррентное соотношение для коэффициентов.
class Div(Series):
"Деление рядов"
def __init__(self,a,b):
assert b[0]!=0
self.a=a
self.b=b
self.l=[a[0]/b[0]]
def __repr__(self):
return f'Div({repr(self.a)},{repr(self.b)})'
def step(self):
n=len(self.l)
self.l.append((self.a[n]-sum(self.b[k]*self.l[n-k] for k in range(1,n+1)))/self.b[0])
Что если мы хотим посчитать $e^{\sin x}$? Для этого в ряд для $e^x$ вместо $x$ мы подставляем ряд для $\sin x$. Для этого второй ряд должен начинаться с члена $\sim x$ (или с более высокой степени $x$). Коффициенты ряда-результата наиболее просто выражаются через полиномы Белла от коэффициентов этого второго ряда. Полиномы Белла реализованы во вспомогательном классе, определённом позже.
class Apply(Series):
"a(b)"
def __init__(self,a,b):
assert isinstance(b,Series) and b[0]==0
self.a=a
self.b=b
self.l=[a[0]]
self.bell=Bell()
self.c=1
def __repr__(self):
return f'Apply({repr(a)},{repr(b)})'
def step(self):
n=len(self.l)
self.c*=n
self.bell.step(self.c*self.b[n])
r=0
c=1
for k in range(1,n+1):
c*=k
r+=c*self.a[k]*self.bell[n,k]
self.l.append(r/c)
Очень часто мы хотим вчесто $x$ подставить в ряд $c x$ (например, $-x$). Это можно, конечно, сделать при помощи Apply и второго ряда вида Series([0,c]). Но такое забивание гвоздей микроскопом очень неффективно. Сделаем проще.
class Apply1(Series):
"a(c*x)"
def __init__(self,a,c):
self.a=a
self.c=c
self.x=c
self.l=[a[0]]
def __repr__(self):
return f'Apply1({repr(self.a)},{repr(self.c)})'
def step(self):
n=len(self.l)
self.l.append(self.x*self.a[n])
self.x*=self.c
Это один из обещанных вспомогательных классов (иногда он может пригодиться и сам по себе). Он умножает ряд $a$ на $x^n$. Если $n<0$, то первые $n$ коэффициентов ряда $a$ должны быть равны 0, иначе получится ряд Лорана.
class Shift(Series):
"a*x^n"
def __init__(self,a,n):
if n<0:
for i in range(-n):
assert a[i]==0
self.l=[a[-n]]
self.n=-n
else:
self.l=[0 for i in range(n)]
self.n=-1
self.a=a
def __repr__(self):
return f'Shift({repr(self.a)},{repr(self.n)})'
def step(self):
self.n+=1
self.l.append(self.a[self.n])
Допустим, мы хотим из ряда для $\sin x$ получить ряд для $\arcsin x$, т.е. решить уравнение $\sin x = y$ относительно $x$ в виде ряда по $y$. Это делает класс Inv (в нём опять используются полиномы Белла). Конечно, чтобы задача имела решение, исходный ряд должен начинаться с члена $\sim x$.
class Inv(Series):
"Решить уравнение a(x)=y в виде ряда по y"
def __init__(self,a):
assert a[0]==0 and a[1]!=0
self.a=a
self.l=[0,1/a[1]]
self.bell=Bell()
self.f=1
self.c=1
def __repr__(self):
return f'Inv({repr(self.a)})'
def step(self):
n=len(self.l)
self.bell.step(self.f*self.a[n]/self.a[1])
self.f*=n
self.c/=(n*self.a[1])
r=0
c=1
for k in range(1,n):
c*=1-n-k
r+=c*self.bell[n-1,k]
self.l.append(self.c*r)
Вот парочка очень простых классов, вычисляющих производную и интеграл от ряда.
class Diff(Series):
"Производная"
def __init__(self,a):
self.a=a
self.l=[a[1]]
def __repr__(self):
return f'Diff({repr(self.a)})'
def step(self):
n=len(self.l)+1
self.l.append(n*self.a[n])
class Int(Series):
"Интеграл"
def __init__(self, a):
self.a = a
self.l = [0]
def __repr__(self):
return f'Int({repr(self.a)})'
def step(self):
n = len(self.l)
self.l.append(self.a[n-1]/Fraction(n))
Полиномы Белла вычисляются при помощи рекуррентного соотношения. Этот класс тоже реализован как ленивый.
class Bell:
"""
Bell polynomials $B_{n,k}(x_1,...,x_{n-k+1})$ ($k \le n$)
https://en.wikipedia.org/wiki/Bell_polynomials
"""
def __init__(self):
self.x=[]
self.b={(0,0):Fraction(1)}
def __getitem__(self,n):
return self.b[n]
def step(self,x):
"""
Add a new $n$ (with its $x_n$)
and calculate all $B_{n,k}$ for $k\in[0,n]$
"""
self.x.append(x)
n=len(self.x)
self.b[n,0]=0
c=Fraction(1,n)
for k in range(1,n+1):
r=0
c=1
for i in range(1,n-k+2):
r+=c*self.x[i-1]*self.b[n-i,k-1]
c*=Fraction(n-i,i)
self.b[n,k]=r
Это вспомогательная функция, используемая в классе Pow. Если степень нецелая, т.е. равна $m/n$, то ведущий коэффициент ряда надо возвести в такую степень, что не всегда возможно в классе рациональных чисел. Эта функция пытается возвести целое число $x$ в степень $1/n$ (где $n$ целое) и получить целый результат. Она сначала возводит в степень в числах с плавающей точкой. Это даёт приближённый результат, переводим его в целый с помощью round и проверяем, получили ли мы то, что нужно. Это, конечно, некузяво: когда $x$ и $n$ очень большие целые числа, ошибка вычисления в double precision может стать $>1$, и мы промахнёмся. Но мне было лень придумывать более правильную функцию.
def pow1(x,n):
"x**(1/n)"
y=round(x**(1/n))
assert y**n==x
return y
Посмотрим, как всё это работает.
c=Cos()
s=Sin()
r=c**2+s**2
print(r)
print(r[10])
print(r)
Программа работы с рядами, конечно, не знает, что $\cos^2 x + \sin^2 x = 1$ точно.
Ряд-результат - это дерево, листья которого - объекты Cos() и Sin().
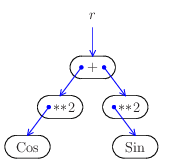
В начале мы видим только, что $r_0 = 1$. Когда мы запрашиваем $r_1$, вызывается r.step(), чтобы вычислить следующий коэффициент. Этот метод вызывает step обоих слагаемых; те, в свою очередь, вызывают step своих аргументов - объектов Cos() и Sin(). И так повторяется каждый раз, когда мы хотим узнать очередной член $r$.
Посчитаем тангенс и арктангенс.
t=s/c
at=t.inv()
print(at)
print(at[10])
print(at)
atd=at.diff()
u=atd[10]
print(atd)
x=Series([0,1])
d=1/(1+x**2)
u=d[10]
print(d)
at=d.int()
u=at[10]
print(at)
Теперь посчитаем $\sin(\tan(x))-\tan(\sin(x))$.
r=s(t)-t(s)
print(r)
Для того, чтобы объекты класса Series можно было вызывать, как функции, т.е. писать s(t), реализован метод __call__. С какого порядка по $x$ начинается ряд $r$?
p,n=r.norm()
print(f'n={n}, p={p}')
Вызов метода r.norm() представляет ряд $r$ в виде $x^n \cdot p$, где ряд $p = p_0 + O(x)$ начинается с ненулевого члена $p_0 \ne 0$, и возвращает кортеж (p,n). Но если ему подсунуть ряд, все коффициенты которого равны 0 (вроде c**2+s**2-1), он бы зациклился. Чтобы избежать этого, введён максимальный порядок по $x$ (по умолчанию 100).
Вот набор тестов, довольно подробно проверяющий работу нашей программы.
n=10
def zero(s):
for i in range(n):
assert s[i]==0
def test_sincos():
c=Cos()
s=Sin()
# cos(x)**2 + sin(x)**2 = 1
zero(c**2+s**2-1)
# (1+cos(x))/2 = cos(x/2)**2
zero((1+c)/2-c.scale(Fraction(1,2))**2)
# (1-cos(x))/2 = sin(x/2)**2
zero((1-c)/2-s.scale(Fraction(1,2))**2)
# sin(asin(x)) = x, asin(sin(x)) = x
asin=s.inv()
x=Series([0,1])
zero(s(asin)-x)
zero(asin(s)-x)
# 1 + tan(x)**2 = 1/cos(x)**2
t=s/c
zero(1+t**2-1/c**2)
# 2*cos(x)*sin(x) = sin(2*x)
zero(2*c*s-s.scale(2))
# cos(x)**2 - sin(x)**2 = cos(2*x)
zero(c**2-s**2-c.scale(2))
# 2*tan(x/2)/(1+tan(x/2)**2) = sin(x)
t=t.scale(Fraction(1,2))
zero(2*t/(1+t**2)-s)
# (1-tan(x/2)**2)/(1+tan(x/2)**2) = cos(x)
zero((1-t**2)/(1+t**2)-c)
def test_explog():
e=Exp()
l=Log()
# exp(log(1+x)) = 1+x
x=Series([0,1])
zero(e(l)-1-x)
# log(1+(exp(x)-1)) = x
zero(l(e-1)-x)
# cosh(x)**2 - sinh(x)**2 = 1
ch=(e+e.scale(-1))/2
sh=(e-e.scale(-1))/2
zero(ch**2-sh**2-1)
# tanh(x) = (exp(2*x)-1)/(exp(2*x)+1)
th=sh/ch
zero((e.scale(2)-1)/(e.scale(2)+1)-th)
# atanh(x) = 1/2*log((1+x)/(1-x))
ath=th.inv()
zero(ath(th)-x)
zero(th(ath)-x)
zero((l-l.scale(-1))/2-ath)
zero(l-l.scale(-1)-l(2*x/(1-x)))
# asinh(x) = log(sqrt(1+x**2)+x
ash=sh.inv()
zero(l((1+x**2)**Fraction(1,2)-1+x)-ash)
# ((1+x)**(1/3))**3 = 1+x
b=Binom(Fraction(1,3))
zero(b**3-1-x)
b**=Fraction(3,5)
zero(Binom(Fraction(1,5))-b)
test_sincos()
test_explog()